Introduction
Learning objectives: You will learn about significance testing, p-values, type I errors, type II errors, power sample size estimation, and problems of multiple testing.
The previous module dealt with the problem of estimation. This module covers the problem of deciding whether two groups plausibly could have come from the same population. This leads to the idea of significance testing and p-values, concepts much misunderstood.
Read the resource text now which covers significance testing.
Resource text
Consider the data in table 1, from Swinscow and Campbell (2002).
A general practitioner wants to compare the mean of the printers' blood pressures with the mean of the farmers' blood pressures.
Table 1: Mean diastolic blood pressures of printers and farmers
| Number | Mean diastolic blood pressure (mmHg) | Standard deviation (mmHg) | |
| Printers | 72 | 88 | 4.5 |
| Farmers | 48 | 79 | 4.2 |
Null hypothesis and type I error
In comparing the mean blood pressures of the printers and the farmers we are testing the hypothesis that the two samples came from the same population of blood pressures. The hypothesis that there is no difference between the population from which the printers' blood pressures were drawn and the population from which the farmers' blood pressures were drawn is called the null hypothesis, often denoted by H0.
But what do we mean by "no difference"? Chance alone will almost certainly ensure that there is some difference between the sample means, for they are most unlikely to be identical. Consequently we set limits within which we shall regard the samples as not having any significant difference. If we set the limits at twice the standard error of the difference, and regard a mean outside this range as coming from another population, we shall on average be wrong about one time in 20 if the null hypothesis is in fact true.
If we do obtain a mean difference bigger than two standard errors, we are faced with two choices: either an unusual event has happened or the null hypothesis is incorrect. Imagine tossing a coin five times and getting the same face each time. This has nearly the same probability (6.3%) as obtaining a mean difference bigger than two standard errors when the null hypothesis is true. Do we regard it as a lucky event or suspect a biased coin? If we are unwilling to believe in unlucky events, we reject the null hypothesis, in this case that the coin is a fair one.
To reject the null hypothesis when it is true is to make what is known as a type I error. The level at which a result is declared significant is known as the type I error rate, often denoted by α. We try to show that a null hypothesis is unlikely, not its converse (that it is likely), so a difference which is greater than the limits we have set, and which we therefore regard as "significant", makes the null hypothesis unlikely.
However, a difference within the limits we have set, and which we therefore regard as "non-significant", does not make the hypothesis likely. To repeat an old adage, 'absence of evidence is not evidence of absence'. A range of not more than two standard errors is often taken as implying "no difference", but there is nothing to stop investigators choosing a range of three standard errors (or more) if they want to reduce the chances of a type I error.
Testing for differences of two means
To find out whether the difference in blood pressure of printers and farmers could have arisen by chance, the general practitioner puts forward the null hypothesis that there is no significant difference between them. The question is, how many multiples of its standard error does the difference in means represent? Since the difference in means is 9 mmHg and its standard error is 0.81 mmHg, the answer is: 9/0.805 = 11.2.
We usually denote the ratio of an estimate to its standard error by "z", that is, z = 11.2. Reference to normal distribution tables shows that z is far beyond the figure of 3.291 standard deviations, representing a probability of 0.001 (or 1 in 1000). The probability of a difference of 11.1 standard errors or more occurring by chance is therefore exceedingly low, and, correspondingly, the null hypothesis that these two samples came from the same population of observations is exceedingly unlikely. The probability is known as the p value and may be written p <<0.001 (where << means much smaller than).
It is worth recapping this procedure, which is at the heart of statistical inference. Suppose that we have samples from two groups of subjects, and we wish to see if they could plausibly come from the same population. The first approach would be to calculate the difference between two statistics (such as the means of the two groups) and calculate the 95% confidence interval. If the two samples were from the same population we would expect the confidence interval to include zero 95% of the time. Hence, if the confidence interval excludes zero, we suspect that they are from a different population.
The other approach is to compute the probability of getting the observed value, or one that is more extreme, if the null hypothesis were correct. This is the p value. If this is less than a specified level (usually 5%) then the result is declared significant and the null hypothesis is rejected.
These two approaches, the estimation and hypothesis testing approaches, are complementary. Imagine if the 95% confidence interval just captured the value zero. What would be the p value? A moment's thought should convince us that it is 2.5%. This is known as a one sided p value, because it is the probability of getting the observed result or one bigger than it. However, the 95% confidence interval is two sided, because it excludes not only the 2.5% above the upper limit but also the 2.5% below the lower limit. To support the complementarity of the confidence interval approach and the null hypothesis testing approach, most authorities double the one sided p value to obtain a two sided p value.
Alternative hypothesis and type II error
It is important to realise that when we are comparing two groups, a non-significant result does not mean that we have proved the two samples come from the same population - it simply means that we have failed to prove that they do not come from the population. When planning studies, it is useful to think of what differences are likely to arise between the two groups, or what would be clinically worthwhile.
For example, what do we expect to be the improved benefit from a new treatment in a clinical trial? This leads to a study hypothesis, which is a difference we would like to demonstrate. To contrast the study hypothesis with the null hypothesis, it is often called the alternative hypothesis and is denoted by H1. If we do not reject the null hypothesis when in fact there is a difference between the groups, we make what is known as a type II error, often denoted as β . The power of a test is defined as 1 - β, and is the probability of rejecting the null hypothesis when it is false. The most common reason for type II errors is that the study is too small.
The relationship between type I and type II errors is shown in table 2. Imagine a series of cases, in some of which the null hypothesis is true and in some of which it is false. In either situation we carry out a significance test, which sometimes is significant and sometimes not. The concept of power is only relevant when a study is being planned. After a study has been completed, we wish to make statements not about hypothetical alternative hypotheses but about the data, and the way to do this is with estimates and confidence intervals.
Table 2: Relationship between type I and type II errors
| Null hypothesis False |
Null hypothesis True |
||
| Test Result | Significant Not significant |
Power Type II error |
Type I error |
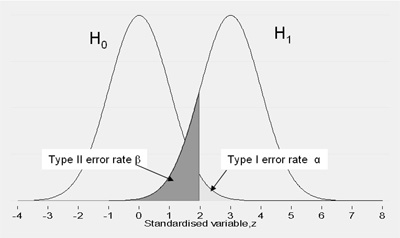
This relationship is illustrated in Figure 1. This shows the expected distribution of a difference between two groups under H0 and H1. It should be clear that, everything else being equal, if we increase the type I error rate we reduce the type II error rate and vice versa
Figure 1 Relationship between type I and type II error rates
Steps to calculating sample size
The first step in deciding a sample size for a study is to decide the primary outcome variable. The significance level should be predefined (5% or 1%). In general this will relate to a two-sided test. Select the power you want the study to have. Usually this is 80% or 90% (i.e. type II error of 10-20%).
For continuous data, find the standard deviation of the outcome measure. This could be achieved by a review of the literature.
For binary data, find the incidence of the outcome in the control group (for a trial) or in the non-exposed group (for a case-control study or cohort study).
Choose an effect size. This is the size of the effect that would be 'clinically' meaningful. This is usually a difficult choice and may be based on a review of previous literature. For example, if a quality of life measure the SF36 is chosen, it is commonly accepted that a difference of 10 percentage points is clinically important. Another way of looking at it is the sort of result from a clinical trial that would make a convincing case for changing treatments. In a cohort study, it might be the size of risk that implies a public hazard.
For instance, suppose we have two groups of subjects randomised to receive either therapy A or therapy B. We choose some outcome for each of the groups to measure the effect of these therapies - say average systolic blood pressure for each of the groups - and want to be able to pick up a difference of (µ0- µa) in mean blood pressure between the groups. Assume that the variance of systolic blood pressure measurements is σ2 and that we wish to perform a test using an α-level of significance and a power of 1 - β. Let zα/2 and zβ be the values corresponding to the chosen power and significance level.
Then the number of subjects required in each group is given by:
n = 2σ2(zα/2+zβ)2/(µ0- µa)2.
Note that the number of subjects required is inversely proportional to the size of the difference we want to detect. The smaller the anticipated difference, the higher the number of subjects we will need.
From this we can see that a larger sample will generally be able to detect smaller differences than a smaller sample. Sample size tables (e.g. Machin et al 2008) or a computer program can help to deduce the required sample size. Often some negotiation is required to balance the power, effect size and an achievable sample size. You should always adjust the required sample size upwards to allow for dropouts.
Problems of multiple testing
Imagine carrying out 20 trials of an inert drug against placebo. There is a high chance that at least one will be statistically significant. It is this one that will be published. The problem of multiple testing happens when:
i) Many outcomes are tested for significance
ii) In a trial, one outcome is tested a number of times during the follow up
iii) Many similar studies are being carried out at the same time
The ways to combat this are:
i) To specify clearly in the protocol which are the primary outcomes (few in number) and which are the secondary outcomes
ii) To specify at which time interim analyses are being carried out, and to allow for multiple testing
iii) To do a careful review of all published and unpublished studies
A useful technique is the Bonferroni correction. This states that if you are conducting n independent tests you should specify the type I error rate as α/n rather than α . Thus, if there are 5 independent outcomes, you should declare a significant result only if the p -value attached to one of them is less than 1%. This test is conservative, i.e. less likely to give a significant result, because tests are rarely independent. An article outlining the issues in this debate can be found by Perneger: 'What's Wrong with the Bonferroni method?' at http://www.bmj.com/cgi/content/full/316/7139/1236.
Video 1: A video demonstrating type 1 and type 2 errors. (This video footage is taken from an external site. The content is optional and not necessary to answer the questions.)
References
- Achin D, Campbell MJ, Tan S-B, Tan S-H, (2008) Sample Size Tables for Clinical Studies. Blackwell Scientific Publishing.
Swinscow TDV and Campbell MJ Statistics at Square One 10th Ed. Blackwell BMJBooks 2002.
Perneger T, What's wrong with Bonferroni adjustments? BMJ 1998;316:1236-1238.
