PLEASE NOTE:
We are currently in the process of updating this chapter and we appreciate your patience whilst this is being completed.
The randomised controlled trial (RCT) is widely recognised as the gold standard design for assessing the effectiveness of healthcare interventions. In many cases, these interventions are delivered by providers to groups of individuals. In this situation it is often more practical to randomise groups or clusters of individuals to an intervention, rather than allocating patients individually. Examples of so-called cluster RCTs might include:
- Randomising family units when assessing a dietary intervention, to avoid the possibility of different members of the same family being assigned to different interventions.
- In a trial of a smoking cessation intervention delivered by GPs, it may also be more practical to randomise the GP practices to one of the interventions. Asking the same GP to deliver two entirely different interventions is impractical, and additionally patients of the same physician may be acquainted.
The main feature of such interventions is that patients are nested within larger clusters, or groups, such as GP practices, hospitals or communities. The intervention is applied at the cluster level, while the outcomes are measured at the patient level.
The effects of interventions applied at the cluster level might be greater than the sum of effects on individuals, for example social networks reinforcing health promotion messages or herd immunity in immunisation programmes. Clustering according to established groups may also reduce the risk of contamination, for example if patients in different treatment arms discuss their respective interventions.
Whilst this chapter focuses on clustering within RCTs, it should be noted that clustering of data can occur in other situations, for example in longitudinal studies where repeated observations are made on the same individuals over time, or where clustered sampling is utilised in deriving subjects for surveys.
Statistical considerations
Because individuals within clustered data are not fully independent of each other, cluster RCTs require special statistical considerations when designing the trial, and later when analysing the data.
Such trials are not as statistically efficient as standard RCTs. Groups tend to form because of certain selection factors, so individuals within the group tend to be more similar to each other with respect to important potential confounders than those selected truly at random.
Examples of this include:
- Patients seen by the same GP are more likely to receive similar treatment for a given condition than those being treated for the same condition by different doctors.
- Patients attending a single GP practice are likely to share similarities including geography, socioeconomic status, ethnic background, or age by virtue of the area they have all chosen to live
- In the same way, GPs who have chosen to work together are likely to share similarities
Similarities, or homogeneity, between subjects in clusters reduces the variability of their responses, compared with that expected from a random sample. This results in a loss of statistical power to detect a difference between the intervention and control groups. A compensatory increase in sample size is required to maintain power in a cluster RCT, and the degree of similarity within clusters should also be assessed.
Intra-cluster correlation coefficient (ICC)
The intra-cluster correlation coefficient (ICC) is a measure of the relatedness, or similarity, of clustered data. It is depicted by the Greek letter rho – ρ.
There are different methods of calculating the ICC, usually requiring a pilot study, but all compare the variance within clusters with the variance between clusters.
Example:

Values of ρ range from 0 to 1 in human studies, and as the ICC increases the more individuals within the clusters resemble one another.
- If ρ = 1, all responses within a cluster are identical and the effective sample size is reduced to the number of clusters rather than the number of individuals
- If ρ = 0, there is no correlation of responses within a cluster, and individuals within and amongst the group are independent with respect to that variable
As the ICC increases, the sample size required to detect a significant difference for the variable under investigation increases.
Design effect and effective sample size
Because of similarities amongst subjects within a cluster, there is a net loss of data. For example, if a trial includes four GP practices, each enrolling 25 patients, there are 100 subjects in the study. However, from a statistical perspective, similarities between subjects in the same cluster effectively reduces the number of participants in the trial. If the ICC is large, there may be far fewer subjects enrolled “statistically”.
If the ICC is known, for example from a pilot study, it can be used at the design stage of the trial to inform the sample size calculation. The ‘design effect’ (DE) can be used to estimate the extent to which the sample size should be inflated to accommodate for the homogeneity in the clustered data:
DE = 1+(n-1)ρ
n = average cluster size ρ = ICC for the desired outcome
The DE can then be used to calculate the ‘effective sample size’. This is the ‘real’ sample size in a clustered trial, compared with the number of participants actually enrolled in the study. It is calculated using the formulae below:

In the example above, there were 4 GP practices recruiting 25 patients each. Assuming the ICC (ρ) = 0.017, the effective sample size is calculated below as:
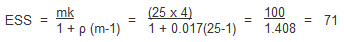
The effective sample size is reduced to 71, compared with the 100 participants enrolled in the trial.
Analysis
In studies where there is clustering, these can be statistically accounted for. Cluster-robust standard errors are a form of standard error that account for the effects of clustering, generating larger values with subsequently wider confidence intervals and more conservative p values. Regression models can also be adapted to account for clustering, using either fixed effects models (where the cluster itself is included as a factor within a standard regression model) or random effects models (which account for the similarities between individuals within clusters in a multilevel model).
Advantages
- Appropriate for public health interventions where a population or group is the unit of randomisation and intervention
- May be cheaper, quicker and more straightforward to conduct
Disadvantages
- More complex design to take account of intra-cluster correlation (ICC)
- More complex analysis because there are two levels of inference rather than one - the cluster level and the individual level
- Greater sample size needed to achieve sufficient statistical power, with associated cost implications
- Requires necessary skills in design and analysis
- May be more complex to assess generalisability – for example are the results applicable to clusters, individuals or both?
© Helen Barratt, Maria Kirwan 2009, Saran Shantikumar 2018
