The validity of a screening test
The measures of sensitivity and specificity describe how well the proposed screening test performs against an agreed 'Gold Standard' test. In medicine, a gold standard test or criterion standard test is a diagnostic test or benchmark that is regarded as definitive. This can refer to diagnosing a disease process, or the criteria by which scientific evidence is evaluated. The actual gold standard test may be too unpleasant for the patient, too impractical or too expensive to be used widely as a screening test.
Assessment of test performance is usually presented in a two by two table (3.2.1). The disease status (as assessed through the Gold Standard) is conventionally put in the top row and the screening test result in the first column.
Table 3.2.1
|
|
Disease status as determined by 'Gold Standard' |
|||
|
Disease |
No Disease |
|
|
|
|
Test positive |
True positives (a) |
False positives (b) |
Total test positives (a+b) |
|
|
Test negative |
False negatives (c) |
True negatives (d) |
Total test negatives (c+d) |
|
|
|
Total with disease (a+c) |
Total without disease (b+d) |
Total screened (a+b+c+d) |
|
|
|
|
|
||
True positives = number of individuals with disease and a positive screening test (a)
False positives = number of individuals without disease but have a positive screening test (b)
False negatives = number of individuals with disease but have a negative screening test (c)
True negatives = number of individuals without disease and a negative screening test (d)
Sensitivity and specificity
Sensitivity is defined as the ability of the test to detect all those with disease in the screened population. This is expressed as the proportion of those with disease correctly identified by a positive screening test result.
| Sensitivity = | number of true positives | = a/ (a+c) | |
| total with disease |
Specificity is defined as the ability of the test to identify correctly those free of disease in the screened population. This is expressed as the proportion of those without disease correctly identified by a negative screening test result.
| Specificity = | number of true negatives | = d/ (b+d) | |
| total without disease |
Positive and negative predictive values
The positive predictive value (PPV) describes the probability of having the disease given a positive screening test result in the screened population. This is expressed as the proportion of those with disease among all screening test positives.
| PPV = | number of true positives | = a / (a+b) | |
| total test positives |
The negative predictive value (NPV) describes the probability of not having the disease given a negative screening test result in the screened population. This is expressed as the proportion of those without disease among all screening test negatives.
| NPV = | number of true negatives | = d / (c+d) | |
| total test negatives |
The effect of disease prevalence
Sensitivity and specificity are independent of prevalence of disease, i.e. test specific (they describe how well the screening test performs against the gold standard).
PPV and NPV however are disease prevalence dependant, i.e. population specific. PPV and NPV give information on how well a screening test will perform in a given population with known prevalence. Generally a higher prevalence will increase the PPV and decrease the NPV.
Knowledge of expected disease prevalence in the target population is necessary when a screening activity is introduced to mitigate the potential harms and costs (see ethical, economic, social, legal aspects).
Practical examples using sensitivity, specificity, Gold (reference) Standard, positive predictive value, and negative predictive value (amended from https://onlinecourses.science.psu.edu/stat507/node/71)
A new ELISA (antibody test) is developed to diagnose HIV infections. Serum from 10,000 patients that were positive by Western Blot (the Gold Standard assay) was tested, and 9,990 were found to be positive by the new ELISA screening test. The manufacturers then used the ELISA to test serum from 10,000 nuns who denied risk factors for HIV infection. 9,990 were negative and the 10 positive results were negative by Western Blot.
Test performance assessment populations
|
|
HIV |
||
|
Infected |
Not infected |
||
|
ELISA test |
+ |
9,990 (a) |
10 (b) |
|
- |
10 (c) |
9,990 (d) |
|
|
|
10,000 (a+c) |
10,000 (b+d) |
|
|
Sensitivity = a/(a+c) |
Specificity= b/(b+d) |
||
With a sensitivity of 99.9% and a specificity of 99.9%, the ELISA appears to be an excellent test.
Application to population level
The test is applied to a million people where 1% are infected with HIV (assuming the sensitivity and specificity remain the same) (Table 1). Of the million people, 10,000 would be infected with HIV. Since the new ELISA is 99.9% sensitive, the test will detect 9,990 (true positives - a) people who are actually infected and miss 10 (false negative - c). Looking at those numbers the test appears very good because it detected 9,990 out of 10,000 HIV infected people. But there is another side to the test. Of the 1 million people in this population, 990,000 are not infected. Looking at the test results of the HIV negative population (the specificity of the assay is 99.9%), 989,010 are found to be not infected by the ELISA (true negatives - d), but 990 individuals who are found to be positive by the ELISA (false positives - b). If these test results were used without confirmatory tests (the gold standard Western Blot), 990 people or approximately 0.1% of the population would have been told that they are HIV infected when in reality, they are not.
(Table 1)
|
1% Prevalence |
HIV |
|
|||
|
Infected |
Not infected |
||||
|
Test |
+ |
9990 (a) |
990 (b) |
Test positives |
Positive Predictive Value= a/(a+b) |
|
- |
10 (c) |
989,010 (d) |
Test negatives |
Negative Predictive Value= d/(c+d) =989,010/(10+989,010) |
|
|
|
HIV positive |
HIV negative |
Total screened= |
||
|
Sensitivity = 99,9% |
Specificity |
|
|||
Sensitivity and specificity are not the only performance features because they do not address the problems of the prevalence of disease in different populations. For that, the understanding of the positive and negative predictive value is crucial. The paragraphs below outline the effects of prevalence on the predictive value of test results in two different populations.
Population A
Blood donors have already been screened for HIV risk factors before they are allowed to donate blood, so that the HIV sero-prevalence in this population is closer to 0.1% instead of 1% (Table 2). For every 1,000,000 blood donors, 1,000 are HIV positive. With a sensitivity of 99.9%, the ELISA would pick up 999 of those thousand, but would fail to pick up one HIV sero-positive individual. Of the 999,000 uninfected individuals, the test would label 998,001 individuals as sero-negative (true negatives). The ELISA would, however, falsely label 999 individuals as sero-positive (false-positives). Testing the blood donor pool results in as many false positive as true positive results.
(Table 2)
|
0,1% Prevalence |
HIV |
|
|||
|
+ |
- |
||||
|
Test |
+ |
999 (a) |
999 (b) |
Test positives |
Positive Predictive Value= |
|
- |
1 (c) |
998,001 (d) |
Test negatives |
Negative Predictive Value= |
|
|
|
HIV positive |
HIV negative |
Total |
||
|
Sensitivity |
Specificity |
|
|||
Population B
The second population consists of former IV drug users attending drug rehabilitation units, with a prevalence of 10% (Table 3). For a million of these individuals, 100,000 would be HIV-infected and 900,000 would be HIV negative. The HIV ELISA would yield 99,900 true positives and 100 false negatives. Of the 900,000 HIV negative individuals, the ELISA will find 899,100 to be negative but falsely label 900 as positive.
(Table 3)
|
10% Prevalence |
HIV |
|
|||
|
+ |
- |
||||
|
Test |
+ |
99,900 |
900 |
Test positives |
Positive Predictive Value= |
|
- |
100 |
899,100 |
Test negatives |
Negative Predictive Value= |
|
|
|
HIV negative |
HIV negative |
Total screened= |
||
|
Sensitivity |
Specificity |
|
|||
Summary of example
The sensitivity and specificity of the test has not changed. It is just that the predictive value of the test has changed depending on the population being tested.
The positive predictive value is how many of the test-positives truly have the disease. In the first example with a 1% sero-positive rate, the ELISA has a positive predictive value of 0.91 (91%). When looking at the blood donor pool with a 0.1% sero-prevalence, the positive predictive value is only 0.5 (50%), whereas in the high-prevalence population of intravenous drug users, the positive predictive value is 0.99 (99%).
Although the sensitivity of the ELISA does not change between populations, the positive predictive value changes drastically from only half the people that tested positive being truly positive in a low-incidence population to 99% of the people testing positive being truly positive in the high-prevalence population. The negative predictive value of the ELISA also changes depending on the prevalence of the disease.
False positive results produced by high sensitivity of the screening test can easily be excluded by a confirmatory test with high specificity.
Information on the possibility of false positive results and subsequent action should be provided to individuals prior to being screened (see informed consent).
The use of receiver operating characteristic (ROC) curves
The two most common uses of ROC curves in medicine are:
- to set a cut-off value for a test result (for continuous diagnostic variables)
- to compare the performance of different tests measuring the same outcome (test validation)
In order to set the cut-off value for a continuous diagnostic variable (e.g. blood lactate level as a marker for risk of death in A&E admissions) the proportion of true-positives and false-positives are calculated for possible values. These proportions are sensitivity and 1-specificity. The ROC curve is a graphical display of how the proportions of true positives and false positives change for each of the possible pre-determined values.
The choice of a particular cut-off value for a test is essentially a decision informed by the attempt to maximise sensitivity and specificity. Generally, there is a trade-off between sensitivity and specificity, and the decision must be based on their relative importance. However, the decision to use a diagnostic test depends not only on the ROC analysis but also on the ultimate benefit to the patient. The prevalence of the outcome, which is the pre-test probability, must also be known.
In situations where there are multiple laboratory tests for a particular condition, the area under each respective ROC curve (AUROC) can be used to compare the overall performance of those tests. The perfect test would have an AUROC of 1, whereas a test with no diagnostic capability would have an AUROC of 0.5. An AUROC of 0.5 indicates that a test based on that variable would be equally likely to produce false positive or true positive results. This equality is represented by a diagonal line from (0,0) to (1,1) on the graph of the ROC curve. The AUROC is usually calculated with statistical packages.
The figure below shows an example of ROC curves for both lactate and urea as markers for risk of death. Visual inspection of the figure suggests that urea is a better diagnostic variable than lactate:
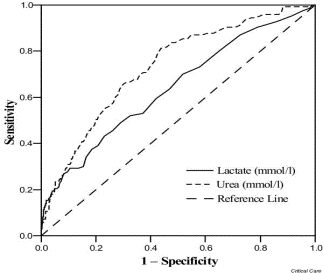
Receiver operating characteristic (ROC) curves for lactate and urea.
Bewick et al. Critical Care 2004 8:508 doi:10.1186/cc3000
A ROC curve can demonstrate several things:
- It shows the trade-off between sensitivity and specificity (any increase in sensitivity will be accompanied by a decrease in specificity and vice-versa).
- The closer the curve follows the left-hand border and then the top border of the ROC space, the more accurate the test.
- The closer the curve comes to the 45-degree diagonal of the ROC space, the less accurate the test.
- The area under the curve (AUROC) can be used to assess test accuracy, and to compare the performance of different tests.
Summary
ROC analysis provides a useful mean to assess the diagnostic accuracy of a test and to compare the performance of more than one test for the same outcome. However, the usefulness of the test must be considered in the light of the clinical circumstances.
Origin of ROC
'ROC analysis is part of a field called "Signal Detection Theory" developed during World War II for the analysis of radar images. Radar operators had to decide whether a blip on the screen represented an enemy target, a friendly ship, or just noise. Signal detection theory measures the ability of radar receiver operators to make these important distinctions. Their ability to do so was called the 'Receiver Operating Characteristics'.
© Dr Murad Ruf and Dr Oliver Morgan 2008, Dr Kelly Mackenzie 2017
