Introduction
Learning objectives: You will learn about Kaplan-Meier survival curves, log-rank tests, and Cox regression.
Survival analysis is concerned with the time elapsed from a known origin to either an event or a censoring point. It may deal with survival, such as the time from diagnosis of a disease to death, but can refer to any time dependent phenomenon, such as time in hospital or time until a disease recurs. The latter is often termed disease-free survival. The techniques of survival analysis are used in clinical trials and in cohort studies.
Please now read the resource text below.
Resource text
A key feature of survival analysis is the concept of a censored observation. This is one where the event in question (such as death or discharge from hospital) has not happened at the time of the analysis, and all we know is the length of time the subject has been in the study. We assume that the reason for a subject being censored is independent of the factors under study. This is known as non-informative censoring. Censored observations occur in two main ways:
i) Before the study completes, a subject may withdraw, or be lost to follow up
ii) On completion of the study, subjects who have not yet experienced an event
An important assumption in survival analysis is that the censoring is uninformative. What this means is that their probability of being censored is unrelated to the probability of having an event. For example, if terminally ill people are moved to a hospice where they are lost to follow up-this would be informative censoring.
The best way to display survival data is a Kaplan-Meier survival curve. This has the probability of survival on the vertical axis, and time on the horizontal axis. Every time an event occurs the survival curve is re-calculated. In contrast an actuarial survival curve calculates survival at fixed points of time, such as annually.
A risk is the probability of an event happening over a period of time. Imagine, however, that the risk varies over time. Then a hazard is the risk estimated at a particular point in time. An analogy would be to measure the speed of a vehicle by finding how far it travels over a fixed period of time. This would give the average speed, which is equivalent to how the risk is measured. The speed shown by the speedometer at each point in time is equivalent to the hazard. The hazard is sometimes referred to as the 'instantaneous probability of failure'.
Hazard ratios quoted in a paper can be interpreted as risk ratios or relative risks.
Comparing survival between two groups
To compare two groups, the equivalent of the Man-Whitney U test is the modified Wilcoxon test. An alternative is the log-rank test. These are both two-sample non-parametric tests which allow for censored observations. They differ in the weight they give to events occurring early or late in the follow up period.
Cox's proportional hazards model
The most commonly used model to analyse survival data is the Cox proportional hazards model. This models the log hazard against a linear predictor of explanatory variables. It is a semi-parametric model, which means that there is no requirement to specify a particular underlying survival distribution, but that the explanatory variables are included in a predefined way in a parametric model. The assumption of proportional hazards means that, in the two-group case, the hazard in one group remains proportional to the hazard in the other over the follow-up time, or equivalently that the relative hazard remains constant. In practice, this requirement means that the survival curves should not cross over.
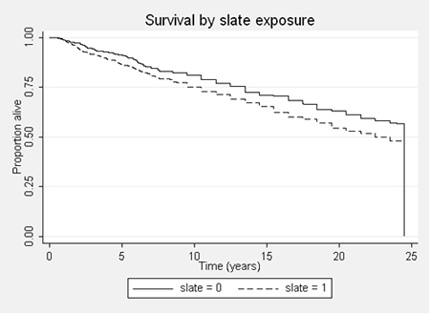
An example of a survival curve is given in the figure. It shows the Kaplan Meier plot of a cohort of slateworkers over 24 years. You can see that a lower proportion of slateworkers are alive compared with controls over the period (Campbell et al. 2005).
A Cox regression of the slate workers study is given in the table. You can see that there is a 24% increased risk of death over the follow-up period in those exposed to slate dust. The second half of the table shows the regression coefficients when smoking history is included in the analysis. It can be seen that the risk of slate dust is unaffected by smoking history.
The main assumption is that this risk is constant over the follow-up period (the proportional hazard assumption). Thus we assume that the risk associated with being a smoker, relative to a non-smoker, stays constant over the follow-up period.
Table: Cox regression on those under 75yrs at first survey. All cause mortality.
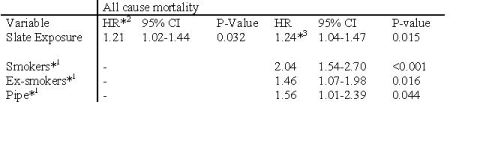
1 Compared to non-smokers.
2 HR=Hazard Ratio
3 Rate adjusted for smoking
References
- Campbell MJ, Oxford Blackwell BMJ Books Chapter 4, 2005. Statistics at Square Two 2nd Ed.
Campbell MJ, Hodges NG, Thomas HF, Paul A, Williams JG. J Occupational Medicine 2005; 55: 448-453A. 24 year cohort study of mortality in slate workers in North Wales.
