Standardisation

Introduction

Learning objectives: You will learn about:

• Direct standardisation
• Indirect standardisation
• issues in the use of standardisation

This section introduces you to standardisation, a method for overcoming the effect of confounding variables in epidemiological research. Most commonly, standardisation is used to control for age. There are two methods of standardisation, direct and indirect, and both are explained here.

Read the resource text now, which covers methods of standardisation and issue in their use.

Resource text

A principal role in epidemiology is to compare the incidence of disease or mortality between two or more populations. However, the comparison of crude mortality or morbidity rates is often misleading because the populations being compared may differ significantly with respect to certain underlying characteristics, such as age or sex, that will affect the overall rate of morbidity or mortality 1.

For example, age is an important determinant of mortality. An older population will have a higher overall mortality rate than a younger population. As a result, variations in age will complicate any comparison between two or more populations that have different age structures.

To understand how a comparison of crude rates can be affected by differing population distributions, it should be recognized that a crude overall rate is simply a weighted average of the individual category specific rates, with the weights being the proportion of the population in each category.

Presentation of category specific rates

One method of overcoming the effects of confounding variables such as age is to simply present and compare the age specific rates. While this allows for a more comprehensive comparison of mortality or morbidity rates between two or more populations, as the number of stratum specific rates being compared increases, the volume of data being examined may become unmanageable.

It is, therefore, more useful to combine category specific rates into a single summary rate that has been adjusted to take into account its age structure or other confounding factor. This is achieved by using the methods of standardisation.

Methods of Standardisation

There are two methods of standardisation commonly used in epidemiological studies, and these are characterized by whether the standard used is a population distribution (direct method) or a set of specific rates (indirect method). Both direct and indirect standardisation involves the calculation of numbers of expected events (e.g. deaths), which are compared to the number of observed events.

Age is a factor that is frequently adjusted for in epidemiological investigations, particularly in comparative mortality studies, since the age structure of a population will greatly affect the population's overall mortality. To illustrate the methods of both direct and indirect standardisation, the age specific mortality rates for two hypothetical populations are compared below.

12. Direct method of standardisation

Table 1 presents crude mortality data for two hypothetical populations (countries A and B). The overall crude mortality rate is higher for country A (10.5 deaths per 1,000 person years) compared with country B (7 deaths per 1,000 person years), despite the age-specific mortality rates being higher among all age-groups in country B.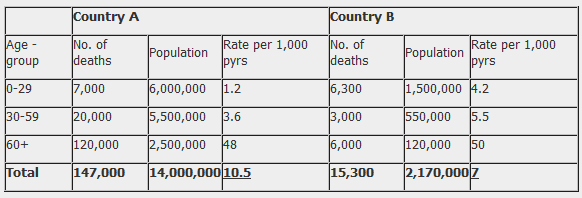

Table 1. Crude mortality rates stratified by age for two hypothetical populations.

Table 2. Direct method of standardisation - calculation of the number of expected deaths for countries A and B applied to a standard population.

(Here the rate is divided back by 1000 to give the basic rate; e.g. 1.2 becomes 0.0012 for the purposes of the formula.)

The reason for the difference between the crude mortality rates between country A and country B is that these two populations have markedly different age-structures. Country A has a much older population than country B. For example, 18% of the population in country A are aged over 60 years compared with 6% in country B.

Table 3. Standard population

In the direct method of standardisation, 'age adjusted rates' are derived by applying the category specific mortality rates of each population to a single standard population (table 3). This produces age standardized mortality rates that these countries would have if they had the same age distribution as the standard population.

Note that the 'standard population' used may be the distribution of one of the populations being compared or may be an outside standard population such as the 'European' or 'World' standard population.

The weighted average of the category-specific rates (with the weights taken from the standard population) provides for each population a single summary rate that reflects the numbers of events that would have been expected if the populations being compared had the same age distribution 1.

The ratio of the directly standardized rates can then be calculated to provide a single summary measure of the difference in mortality between the two populations. The ratio of the standardized rates is called the Comparative Mortality Ratio (CMR) and is calculated by dividing the overall age adjusted rate in country B by the rate in country A. For example:

Comparative Mortality Ratio = 9.6/7.1 = 1.35

This CMR is interpreted as: after controlling for the confounding affects of age, the mortality in Country B is 35% higher than in country A.

Note that while the crude rates presented in table 1 represent the actual mortality experience of countries A and B, it is not possible to use these crude rates to make a valid comparison between the two countries because they have very different age distributions. However, by using the direct method of standardisation (while the values of the adjusted rate do not reflect the 'true' mortality experience of countries A and B), it enables us to calculate 'hypothetical' age adjusted rates that can be used to make a valid comparison of overall mortality between the two countries.

13. Indirect method of standardisation

The indirect method of standardisation is commonly used when age-specific rates are unavailable. For example if we did not know the age specific mortality rates for country B.

In this method, instead of taking one population structure as standard and applying sets of rates to it to estimate expected events, a set of rates from a standard population (country A) is applied to each of the populations being compared to calculate standardized morbidity/mortality ratios.

Table 4. Indirect method of standardisation: Number of expected deaths if the population had the same age-specific mortality rates as Country A.

In table 4, the indirect method of standardisation is used to calculate how many deaths would be expected in Country B if it had the same age-specific mortality rates as Country A.

The expected deaths in Country B are calculated by multiplying the age specific rate for Country A by the population of Country B in the corresponding age group. The sum of the age categories gives the total number of deaths that would be experienced in country B if it had the same mortality experience as country A.

An overall summary measure can then be calculated, that is, the standardized mortality ratio (SMR), which is the ratio of the observed number of deaths to the expected number of deaths.

SMR = Observed number of deaths (O) X 100%
           Expected number of deaths (E)

SMR = 160 = 1.6 X 100 = 160
          100

From table 4 the SMR is calculated as 160, which means that the number of observed deaths in Country B is 60% higher than the number we would expect if Country B had the same mortality experience as Country A.

14. Issues in the use of standardisation

• Standardised rates are used for the comparison of two or more populations; they represent a weighted average of the age specific rates taken from a 'standard population' and are not actual rates.