Health Economics: 5 - Techniques of Economic Appraisal
5.1 What is economic appraisal?
Economic appraisal and economic evaluation are different names given to research studies that weigh the costs of an action against the benefits that it provides. The difference between them is that appraisal is carried out before an action is taken, to help in deciding what is to be done by estimating the effects it is likely to have; and evaluation is carried out after the action is taken, to monitor what effects it actually had. However, this distinction is often forgotten and these labels are used interchangeably. In recent years, the expression ‘evaluation’ has become dominant in the literature on health economics, but ‘appraisal’ is used here because it describes better the kind of research mainly used in health economics.
In economics more generally, this type of research is called cost-benefit analysis (CBA). (However, as will be explained below, in health economics this term is often reserved for a particular technique related to the measurement of social efficiency, as defined in Section 1.4.1.) It is a structured approach to help decision makers choose between alternative ways of using resources. Its aim is to measure efficiency in areas where there is public involvement and there are no market-based measures available to judge issues of efficiency. In principle, equity should be an equally important aspect of every economic appraisal, but there are fewer formal techniques available to analyse this.
An appraisal can be considered as a process with five stages: defining the problem to be analysed; specifying alternative ways of dealing with the problem; assessing the costs and benefits of the alternatives; summarising the results; and deciding.
The problem is always the starting point of an appraisal and must be defined clearly. This point may seem obvious, but it is often the case that the reason why appraisals are carried out is that there is a solution available for a problem. That solution is then wrongly seen as the starting point. For example, appraising the cost-effectiveness of a new drug should be reformulated as an appraisal of what is the most cost-effective way to deal with the problem that the new drug is licensed for. This may have an impact on the second stage, defining alternatives, which means different ways of dealing with the problem. The most relevant alternative should be chosen, whatever it is, for example, another drug, another type of therapy, routine care without specific therapy or do nothing.
Assessing costs and benefits has three stages: itemising costs and benefits, which means drawing up a descriptive list of the costs and benefits that are to be included in the appraisal; measurement, which means obtaining data that describe the levels of costs and benefits for the different alternatives; and valuation which means converting these data into values. For example, resource use data should be converted into costs by applying to those data the value of the resources. Further details of how this is done in practice are given in sections 5.4 and 5.5.
Summarising the results means combining the data on costs and benefits into the results that will be presented to whoever will decide on the problem that has been appraised. Exactly what form this will take depends on the type of appraisal that is carried out - see section 5.3 - and how uncertainty over the results is dealt with - see section 5.6.
The last stage is when a decision is taken based on the appraisal by someone who has the responsibility to make it, which should not be the appraiser. Appraisers often do recommend a decision based on their own appraisal, or imply such a recommendation, which is legitimate if decision rules are known. For example, suppose that there is an accepted decision rule that if the monetary benefits of a health intervention exceed its monetary cost then it should be provided to the population. A finding, for a particular intervention, that its benefits are estimated to be greater than its costs would justify a recommendation that it should be provided.
An important aspect of the relationship between appraisal and decision is that the scope of the appraisal should be a clear, include whose viewpoint is to be taken. Different actors in the health system, for example patients, health professionals and government, may have different interests and concerns, so that what is efficient from one actor’s point of view may not be so from another. This determines key elements of an appraisal, such as which type of appraisal is to be used, what constitutes a benefit and a cost and how these are to be valued. Most appraisals will take the viewpoint of the health service, since that embodies most of those actors who are legitimate decision makers concerning which health care is to be provided. However, appraisals may also take the viewpoint of society as a whole, since that includes both the recipients of health care and also the funders of it. Whatever viewpoint is adopted, those reporting an appraisal should be explicit about which it is.
5.3 Types of economic appraisal
There are some differences in the aims and methods of different economic appraisals, such that they have been classified according to distinct types. However, there are different principles by which they could be classified, which leads to occasional disputes about how results of a particular type of appraisal should be interpreted or used. Three different classification principles are:
- The kind of efficiency they analyse, technical, economic or allocative.
- Which costs and benefits are measured and how this is done.
- The type of decision that they apply to.
We will discuss all three types here, but the most widespread and popular classification in health economics is given by Drummond et al (2015), which uses both the measurement and decision type principles.
Here, we concentrate here on the types of appraisal most likely to be encountered in health care. We refer to what is being appraised as ‘alternatives’, to emphasise that we are interested in the use of economic appraisal in health care to aid decision making about different ways of using health care resources. This includes many kinds of decisions, including alternative ways of delivering health care, different types of health care and different treatment options.
5.3.1 Cost-benefit analysis (CBA)
As stated earlier, CBA is often defined in economics more generally as a generic term for economic appraisal, starting with an inventory of all the costs and benefits of each alternative, whatever they are and whoever incurs them. This can be regarded as a balance sheet in which overall costs and benefits are weighed against each other. Research involves the stages described above in section 5.2: describing costs and benefits, and quantifying and placing a value on them where possible.
However, in health economics CBA is usually restricted, following Drummond et al, to a study in which all costs and benefits are given money values. The rationale for this is that it is only possible to weigh up all the costs and benefits if they are measured in the same unit. In principle, any common unit could be used, but in practice money is an obvious and natural choice, because it is the measure of economic value most used in modern economies. Such a CBA would allow us to calculate the net benefit of each alternative, the difference between benefits and costs, which could of course be negative. Decision making could then be based on which of the alternatives has the greatest net benefit.
Formally, the main decision rule for CBA is that an activity should be undertaken if the sum of the benefits that result is greater than the sum of the costs of undertaking it or, identically, if its net benefit is positive. If only one activity with a positive net benefit can be undertaken (because, for example, there are limited funds), the activity with the highest net benefit should be chosen.
CBA has a theoretical basis in economics. If costs and benefits are measured in the correct way, for example, all costs measure their true opportunity costs, an alternative that has a net benefit is an opportunity for a Pareto improvement. Drummond et al interpret this to mean that CBA is therefore appropriate for answering questions about whether or not a health care programme should be implemented or a treatment should be used, rather than which of a number of alternative programmes or interventions is the most efficient.
Option appraisal (OA) is a term used by the UK Treasury in the guidance that it gives to public bodies about how they should appraise and evaluate projects that are to be paid for from public funds. This guidance is contained in a publication called the ‘Green Book’ (HM Treasury, Multiple years); the distinction between appraisal and evaluation is carefully kept to in this case. OA is usually used for large scale projects requiring a considerable outlay of capital funds, and has a more general name of investment appraisal. However, in principle it applies to all publicly funded activities. It forms the basis for the economic analysis contained in the ‘Policy Impact Assessment’ that the government carries out for any major policy initiatives. An example of this in public health is the Department of Health’s impact assessment published to justify the implementation of the NHS Health Checks programme.
OA is a process in which different options for meeting an objective, defined by the aim of meeting some public need, are generated. CBA is applied to these options and the best solution for meeting the aims is chosen on the basis of the results. For example, an appraisal of a project for building a new hospital would start with the need to provide acute services, generate different options for dealing with that need, which might include a new hospital build, examine the costs and benefits of each alternative and from this derive the economic case for the new building, if it was found to be the best alternative. The economic case for the project would simply be part of a more general project appraisal included affordability and achievability and various types of impact assessment including on health, the environmental and health and safety.
5.3.3 Cost-consequences analysis (CCA)
Cost-consequences analysis (CCA) is a label given to an economic appraisal that uses the more general CBA framework described above, but does not try to conform to the Drummond et al definition by measuring all of the costs and benefits in money terms. In particular, it accepts that there may be benefits that are fundamentally different from each other and cannot be measured in the same units, which distinguishes it from cost-effectiveness analysis, discussed below, which requires a common unit of benefit. In making decisions based on the information provided by a CCA, decision makers will place their own weights on the different benefits and costs, either explicitly or implicitly. CCA is of particular interest in public health because the National Institute for Health and Care Excellence (NICE) in England (see section 8.1) permits the use of CCA for public health interventions unlike other health care, for which it specifies cost-effectiveness analysis. CCA is often referred to as a disaggregated approach, because the benefits and costs are not combined into a single indicator such as net benefit, defined above, or a cost-effectiveness ratio, defined below.
5.3.4 Cost-effectiveness Analysis (CEA)
Cost-effectiveness has a theoretical basis in the analysis of economic efficiency described in Section 1.4.1. One alternative will be preferred to another if it provides greater benefit at the same or lower cost, or costs less to provide the same or greater benefit. This definition does not directly address the question of which of two alternatives is more efficient if one provides greater benefit than the other, but costs less. It is however possible to make such a comparison if certain conditions are met. For example, it may be possible to scale the alternatives up or down to produce the same level of total cost, and compare the resulting level of benefit, or vice versa. However, if there are economies of scale (see section 1.2.3), that would not be legitimate. If these conditions are met, then a cost-effectiveness ratio (CER), defined as costs divided by benefits, can be calculated to compare different alternatives. The CER most often used in health economics is called an incremental CER, or ICER (see section 1.3). This means that the costs and benefits of each alternative are calculated compared with their next best alternative, rather than with a common alternative.
The measurement principle for CEA is that, as with CCA, costs are measured in money values, but benefits are measured in units other than money. However, unlike CCA, all the benefits are measured in the same units, usually because only one type of benefit is considered. The consequence is that costs and benefits are not directly weighed against each other. The ICER shows the cost of obtaining one additional unit of benefit for each alternative. Whether that cost is worth incurring is not directly answered by CEA. So, unlike CBA, which tells us whether health programmes or treatments are an efficient use of resources, CEA tells us which of the possible ways of providing them is the most efficient.
Drummond et al restrict use of the label CEA in two ways. First, they regard CEA to be applicable only when both the costs and benefits of the alternatives differ from each other. Appraisal of cases where benefits are the same for each alternative but costs differ is labelled cost-minimisation analysis (CMA). In practice, although such analyses are quite often carried out and published, the term CMA is rarely used to describe them. Secondly, the measurement of benefits is restricted to be in what Drummond et al call ‘natural’ units, such as numbers of cases detected, changes in clinical measures like blood pressure or changes in undesirable biological markers. This distinguishes CEA from another type of appraisal, labelled cost-utility analysis (CUA), which is discussed below. In this the benefits are measured as changes in health-related quality of life rather than ‘natural’ units.
The decision rules applied to this kind of CEA are hierarchical. First, we should reject any alternatives that are dominated by another alternative or combination of alternatives. Domination means economic efficiency in the strict cost-effectiveness sense described above, where the dominated alternative has greater cost with no greater benefits or lower benefits with no smaller costs. The choice between non-dominated alternatives is more complex. If only one alternative can be chosen, we should choose that with the lowest ICER. Where combinations of more than one alternative can be used, it is in principle necessary to calculate the ICERS for every possible combination to decide which is most efficient. There may also be an additional requirement that the chosen alternative or combination of alternatives must also be below a ceiling ratio, which is an externally-set level of the ICER that must be met if it is to be regarded as cost-effective.
These issues can be illustrated using a cost-effectiveness plane diagram (Black, 1990). ICERs are presented graphically as a combination of the costs and the effects of a health intervention, compared to an alternative, perhaps a different intervention. Costs are conventionally placed on the north-south (top-bottom) axis and effects on the east-west (right-left) axis. In both cases, these effects can be negative, zero or positive:
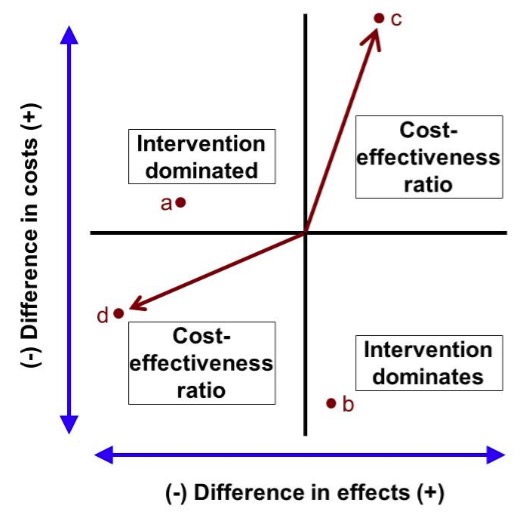
An intervention can be located on this diagram according to its incremental costs and benefits. If it lies in the north-west (top left) quadrant, such as point a, the costs of the intervention are higher than its alternative, and its benefits are lower. It is unambiguously worse than its alternatives, it is dominated and should be rejected. Similarly, in the south-east (bottom right) quadrant, at a point such as b, costs are lower and benefits are higher than its alternatives, so the treatment dominates and should be accepted. In the north-east (top right) quadrant, at a point such as c, higher benefits are gained at a net cost over the alternative, so neither dominates. We can calculate an ICER, the cost per unit of effect gained, measured as the slope of the line from the origin to the point. In the south-west (bottom left) quadrant, at a point such as d, lower costs can be obtained at the expense of lower benefits. Again, neither dominates, and we can calculate an ICER, although this now refers to a cost saving per unit of effect lost. It is again measured as the slope of the line from the origin to the point.
The cost-effectiveness plane diagram can also be used to illustrate the meaning and use of the ceiling ratio, where it is often referred to as demonstrating cost-effectiveness acceptability:
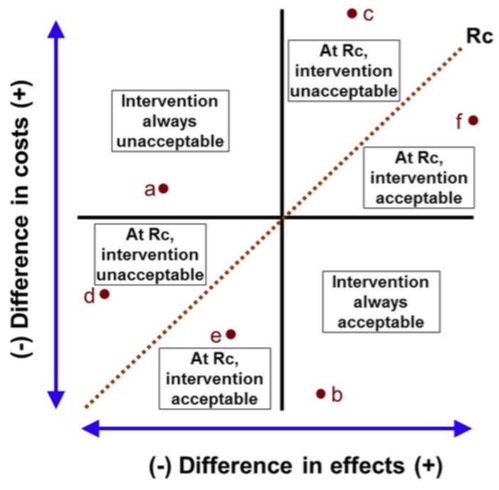
The dotted line Rc shows a given ceiling ratio. If an intervention’s ICER lies above the line, it will not be acceptable on cost-effectiveness grounds. Either it is dominated by the alternative, whatever the ceiling ratio is, as in point a; or its ICER does not satisfy the ceiling ratio, as in points c and d. In the north-east quadrant, this means that the ICER is above the ceiling ratio, as in point c; the higher benefit is outweighed by the higher cost. In the south-west quadrant, it is below, as in point e; the cost saving does not justify the lower effectiveness.
Below the line the intervention is acceptable. This is because either it dominates the alternative, as in point b, or its ICER satisfies the ceiling ratio, as in points e and f. If the ICER is below the ceiling ratio in the north-east quadrant, as in point f, the higher costs are justified by the increased benefits. If it is above in the south-west quadrant, as in point e, the cost savings outweigh the lower benefits.
Ceiling ratios and cost-effectiveness acceptability have an immediate application in analysing decisions based on cost-effectiveness, but they have another more specialised role as a way of handling uncertainty in economic appraisal - see section 5.6.1.
5.3.5 Cost-utility analysis (CUA)
Cost-utility analysis (CUA) is a label used for a special form of CEA in which benefits are measured in terms of changes in Quality-Adjusted-Life-Years (QALYs). QALYs are a composite measure of gains in life expectancy and health-related quality of life; they are discussed in more detail in section 5.5.1. The distinctive outcome of a CUA is the calculation for each an alternative of an ICER in terms of the extra cost per QALY gained (CQG). The label CUA is commonly used in the UK and elsewhere, but rarely in the United States, where CEA includes CQG analyses.
CUA has a more complex rationale than that for CEA. QALYs are regarded by many as a better measure of benefits than ‘natural’ units when appraising therapeutic alternatives for the same condition because they deal with the production of health itself rather than of health care. CUA also offers something that non-QALY CEA cannot, the possibility to compare treatments for different conditions. In principle, treatments for, say, cancer can be compared with, say, physiotherapy, to determine which is the most efficient at producing health gain in the form of QALYs.
This ability that CUA has to compare across all health interventions means that in principle CUA analyses can be used to allocate health care resources between different interventions and to determine health care priorities. This transforms CEA so that it offers the same advantage as CBA in indicating not simply the best way of achieving health care benefits for a particular condition, but whether or not they are worth achieving. Some people therefore regard CUA as a limited form of CBA rather than a special form of CEA. Viewed in this way, CUA is better than CBA, because it avoids having to measure benefits in terms of money.
Section 5.3.4 explained that within a CEA, the ICER of the best alternative is compared to a ceiling ratio. For CUA, the ICER is the CQG, so the ceiling ratio is the amount that it is acceptable to pay to gain a QALY. This is sometimes referred to as a CQG threshold, because it divides health care that is regarded as cost-effective from that which is not. The National Institute of Health and Care Excellence (NICE) has a threshold, though it is not entirely clear what the size of that threshold is (Dakin et al, 2015). This threshold could arise from two different sources. It could reflect the limited budget the NHS has, which determines what can be afforded, known as the shadow price of a QALY. This is the justification given by NICE for its threshold. Alternatively, it could be set to reflect what the population covered by NICE is willing to pay for health gain, known as the social value of a QALY. Whatever the source, if the threshold is known, it can be used to convert costs to QALYs or vice versa, putting costs and benefits into the same units and enabling net benefits to be calculated in the same way as for CBA.
These net benefits can be calculated in terms either of money or of QALYs. To give a hypothetical example, suppose that an intervention has incremental costs of £30,000 and incremental benefits of 2 QALYs. The money value of a QALY can be derived from the ceiling ratio, because in effect it is the price that it is acceptable to pay for a QALY. Suppose that the ceiling ratio is £20,000 per QALY gained. To analyse cost-effectiveness in monetary terms, the QALY gain is multiplied by the ceiling ratio to give the money value of the QALY gain, which is 2x£20,000=£40,000. The net cost is subtracted from this to give a net monetary benefit of £40,000-£30,000 = £10,000. Alternatively, costs can be converted to a QALY gain equivalent by dividing the ceiling ratio by them, giving a net cost equivalent of £30,000/£20,000 = 1.5 QALYs. This means that there is an overall net health benefit of 2-1.5 = 0.5 QALYs. In each case the net benefits are positive, so the intervention is deemed cost-effective.
This is the same result as if we had calculated the ICER to be £30,000/2 = £15,000 and observed that it is below the ceiling ratio of £20,000. There is however an advantage from calculating net-benefits if we do not know the ceiling ratio. We can calculate net benefits for any value of the ceiling ratio, as illustrated in the following diagrams for net monetary and net health benefits:
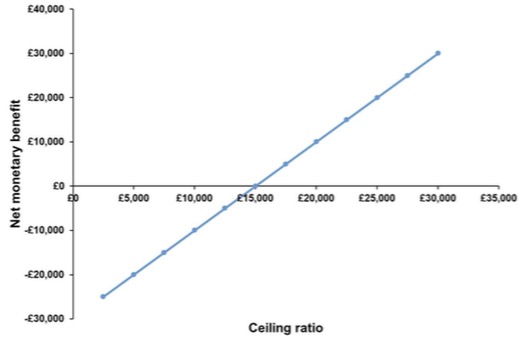
Net monetary benefit curve
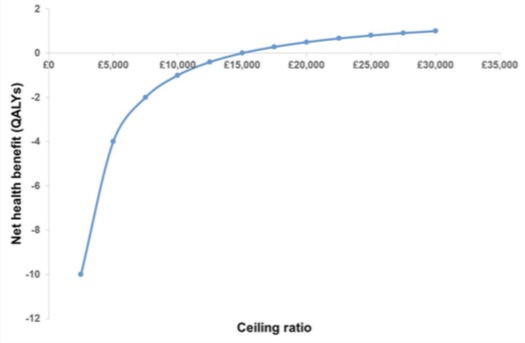
Net health benefit curve
Like cost-effectiveness acceptability, the net benefit approach is also important because it is another way in which uncertainty in economic appraisal is dealt with - see section 5.6.1.
The ability of CUA to compare between different conditions, and thereby to allocate health care resources between different interventions and determine health care priorities is controversial. One problem is that a CEA restricted to different treatments for a particular condition can assume that the patients receiving the treatments are the same people, but this is not true of the comparisons across conditions that CUA permits. Even if such comparisons are valid, they do not simply involve decisions about allocating resources between different health care technologies, but also between different people.
The theory underlying cost-benefit analysis suggests some theoretical principles for the measurement of costs, the most important of which are:
- All costs should be included in the analysis, whatever they are and whoever incurs them;
- Only true opportunity costs should be included; and
- Changes in costs are based on marginal rather than average costs.
These principles are hard, if not impossible, to adhere to. In practice, they are what you’d call guidelines rather than actual rules, a guide to the best sources of cost, if there are alternatives, and to the reliability of the numbers used.
Agreed good practice deriving from the principle of including all costs is to examine costs according to who incurs them, in three categories: the health service; patients and their families; and the rest of society. Good practice preserves the opportunity cost principle by separating costing into an assessment of the use of resources and attaching a value to those resources. This procedure is also good practice for ensuring that research is generalisable, since resource use may be similar in different settings, but the prices paid for those resources may vary considerably. As suggested in section 5.2, the process of costing involves three steps:
- Identifying and describing resource use changes;
- Quantifying resource use in physical units; and
- Valuing resources.
There are two main types of costing: macro or ‘top-down’ costing and micro or ‘bottom-up’ costing, distinguished by the level of aggregation at which individual resources are measured and valued. An example of macro costing would be estimating the costs of a hospital inpatient case for a particular specialty based on aggregate cost data for the hospital overall. Specialty costs could be estimated by allocating a proportion of the total costs to it using an indicator of how costly that specialty is compared with others. For example, if a specialty had 20% of the hospital’s cases, 20% of the costs might be allocated to it. In practice, of course, top-down costing would never be as crude as this. To do the same task using micro-costing, every item of service and every consumable used by every patient in that specialty might be recorded; each item of service would be costed by examining all the time spent on it by every member of staff, as well as the time spent using every piece of equipment; and the cost per case would be built up from those data. Again, in practice, this extreme level of detailed costing is not found. Moreover, costing rarely uses only macro or micro costing. It is common for mixed methods to be used for different elements of cost.
The timing of costs is an important consideration. The fact that resources are used at a particular time and resources are used at different times may affect the way that they are valued, and therefore their costs. There are two important elements to this. First, if costs occur in different years and are measured at the time that they occur, then to make them comparable they should be adjusted for any cost inflation or deflation that has occurred. This ensures that it is the value of resources that is considered, which may be unaffected by the rate of inflation. The best option would be to select one year’s unit costs and apply them to different years’ resource use. That is rarely possible for many items of cost, so best practice is to deflate yearly costs to a common base year by a cost index. For the same reason, if there are any projections of costs for future years from the actual costs measured for the base year, these should not be adjusted to take account of projected inflation.
Secondly, adjusting for inflation means that each year’s costs are measured in the same units of value, those of the base year, but this does not mean that every year’s costs are of the same value when viewed from the base year. The reason for this is that people generally prefer to postpone costs if they can, and a cost incurred now therefore has a higher weight than the same money cost incurred in the future. Looked at another way, future costs have a lower value than the same money costs now. This is dealt with by discounting, which is the application of a time weight to costs so that the further in the future the cost is, the lower is its value. In practice, what is done is to apply a discount rate, which can be viewed as the inverse of an interest rate. An investment that attracts an interest rate results in the investment increasing in value over time. Applying a discount rate means that the value decreases over time. Discounting future costs back to the base year gives their present value.
Timing may be very important in health care, because of the long-lasting effects of many interventions. For example, prevention incurs costs now, and even if it reduces costs in the future by a greater amount, there may not be a net cost saving if the future costs are discounted. Even if there is a net cost saving, it will have a lower value than if discounting was not used. As an extreme example, measures to deal with pre-natal conditions to reduce illness in the later adult life of babies might see cost reductions so many years in the future that discounting would reduce them to a negligible value.
Although there is general agreement that costs should be discounted, there is less certainty about the way that discounting should be done, what the discount rate should be, and how the discount rate should be obtained. For example, there is an unresolved question about whether the discount rate should be held constant over time. There are also two separate theories that underlie measurement of the discount rate for use in public sector decision-making, which may produce different results. One is ‘social opportunity cost’ approach, which assumes that public and private investments compete for resources, so the public sector should use market rates of borrowing. The other is the ‘social rate of time preference’, which measures what people are willing to receive in compensation for delaying consumption from one year to the next. In practice, discount rates for public sector use are usually defined by government; in the UK, the discount rate is set by the Treasury in the ‘Green Book’ referred to in section 5.3.2.
The measurement of effectiveness for CEAs that measure benefits in terms of ‘natural’ units rather than values does not require any special economic analysis. This section is therefore mostly relevant to CUAs, which measure benefits as the value of health gains, and CBAs, which measure benefits as monetary gains. CCAs require different benefits to be measured in ways specific to those benefits, which is too diverse to be covered in detail here.
However, there is an increasingly important benefit measurement method that does not fit neatly into the classification of types of economic appraisal described here and the consequent division between ‘natural’, health and monetary benefits. In a discrete choice experiment (DCE), respondents to a survey are offered a choice between different health interventions, which are described according to attributes that may include health outcomes, other outcomes and the price of the intervention. The choices that the individual respondents make are analysed to reveal the relative values of different attributes to the group of respondents as a whole. This might be used to attribute a value to different health states for a CUA or to calculate the values of different health interventions in terms of money for a CBA, and such applications are briefly described below. However, a DCE might also be used to quantify a non-monetary value for a health intervention, including both health and other benefits.
5.5.1 Measures of benefit in terms of health gain
In this section, we are only concerned with measures of health gain that are suitable for use in economic appraisal. Health and improvements in health can be measured in many different ways and the different ways in which that is done depends on the purposes for which they are being measured. The requirements that economic appraisal have for a measure of health gain directly determine the approaches that are adopted for use in that context.
First, it is useful if an appraisal has an unambiguous indicator of benefit, rather than multiple indicators that may conflict. This implies that the health gain measure should be a single number representing all relevant aspects of health. A single number is of course an essential requirement for calculation of an unambiguous CER. Secondly, appraisal looks at the use of scarce resources that could be devoted to all sorts of health care. The measure of health should therefore be capable of comparing those different uses of resources rather than simply their use in the intervention being appraised. This implies that a ‘generic’ measure of health should be used. Thirdly, appraisal compares costs, which represent the value of the resources used in an intervention, with benefits in terms of health gains. This implies that the measure of health should also be capable of being interpreted as the value of health gains.
There are a few approaches that meet these requirements, the most common of which is the Quality Adjusted Life Year (QALY). This combines the length of life that people have and the quality of their life into a single indicator. The benefit of a health intervention is the gain in QALYs that it produces. Depending on the type of health improvement that an intervention might produce, QALYs can be thought of as an adjustment to years of life gained to account for the quality of life experienced in those years, or the length of time for which an improved quality of life is experienced, or both.
For example, suppose that the prognosis for a person who has been diagnosed as having a particular disease is that they will only live for a further ten years. The first two of those will have a quality of life valued at 60% of full health and the last eight will have a quality of life valued at 40%. If they have a particular treatment, their life expectancy will rise to 12 years, in each of which they will enjoy full health. The number of QALYs that the patient will have without treatment is (2 x 0.6) + (8 x 0.4) = 4.4. The number of QALYs that the patient will have with treatment is (12 x 1) = 12. So, the benefit of the treatment is (12 - 4.4) = 7.6 QALYs gained.
Another measure that has a similar aim and structure is the Disability Adjusted Life Year (DALY), which is promoted by the World Health Organisation and has found widespread use in developing countries in particular, though largely in the context of measuring the burden of illness rather than in economic appraisal (Murray et al, 2012). The DALY is applied to whole populations, combining estimates of life expectancy in the population with the prevalence of disability. This generates an estimate of a ‘health gap’. Improvements in health therefore generate a reduction in DALYs; this is the opposite of QALYs, which are increased by health improvements
A major advantage of using QALYs to assess the impact of health changes is that they can, in principle, be applied to any kind of intervention, whether it raises life expectancy without improving quality of life, improves quality of life without affecting length of life, improves both, or improves one at the expense of lowering the other. However, the assumption underlying this, that length and quality of life can be compared in the same metric is unacceptable to some.
QALYs can be calculated in different ways. It is possible to measure directly the value that patients attach to their quality of life. It is also possible to estimate from other indicators of health a quality of life value. But the most popular approach, which is also recommended by NICE, is to obtain from patients a description of their health state according to a generic health status measure, such as the EQ-5D (Brooks, 1996; Herdman et al, 2011). This results in a descriptive profile of their overall health status, to which can be assigned a common value for each state. The intention is that those values should represent the values of society as a whole, and are commonly taken from a separate survey of a representative sample of the population.
There are different techniques that are used to obtain values within these population surveys. The main four are Rating or Visual Analogue Scales (VAS), Time Trade-off (TTO), Standard Gamble (SG) and the Discrete Choice Experiment (DCE) described earlier.
Using the Visual Analogue Scale method, survey respondents are shown a line, usually with verbal and numerical descriptors at each end of it that describe the meaning of the two ends, such as ‘Best possible health’ and ‘Worst possible health’. Scale markers are often added to the line to denote distance along the line, which are sometimes also numbered. Respondents are given descriptors of a set of health states and are asked to rate the desirability of each of them by placing it at some point on the line on or between the two endpoints.
In the Time Trade-off method, respondents are asked to choose between a number of years in full health and a number of years in a particular health state . The method uses slightly different versions to calculate values from this, depending on whether the states are chronic or acute and whether the respondent believes them to be better or worse than being dead. For a chronic health state preferred to being dead, one of the alternatives is a fixed number of years in the health state; different numbers of years in full health are presented as an alternative. The respondent chooses which they prefer, the number of full health years is changed, and this is repeated until a point is found where the respondent cannot choose between the alternatives. The value for the health state is then calculated as the ratio of the number of years in full health to the number of years in the health state. The reason for this is that it is assumed that when the respondent cannot choose between the two alternatives, the numbers of QALYs generated by them are identical.
In the Standard Gamble method, respondents are offered a choice between the certainty of being in a particular health state and a gamble whose outcomes are full health with a certain probability and death, and asked to choose between them. Again, slightly different versions of this are used depending on whether the states are chronic or acute and whether the respondent believes them to be better or worse than being dead. For a chronic health state preferred to death, different probabilities of being in full health are offered, until the respondent cannot choose between the alternatives. The value for the health state is equal to the probability at that point of indifference. This calculation is based on the expected values of the two alternatives, which is discussed in section 7.
DCEs applied to health state valuation are undertaken by offering respondents a choice between two, or sometimes more, health states and recording their choice. This technique does not measure any individual respondent’s valuations of health states, but infers from the responses of a group their collective valuation.
Generic health state measures are usually accompanied by sets of values for each health state that they define. Because they have so many health states, the values are usually generated by a model, which may be called a multi-attribute utility model, though that label is not explicitly used in some cases and its use in some cases may be disputed. Essentially, health states are decomposed into ‘attributes’. Generic health measures usually describe health states using different ‘dimensions’, in which people can be at different ‘levels’, which form the attributes. For example, one of the most widely used generic measures, the EQ-5D, has in its original “three level” version (Brooks, 1996) the following dimensions and levels:
Mobility
- No problems in walking about.
- Some problems in walking about.
- Confined to bed.
Self-care:
- No problems with self-care.
- Some problems washing or dressing self.
- Unable to wash or dress self.
Usual activities
- No problems with performing usual activities (e.g. work, study, housework).
- Some problems with performing usual activities.
- Unable to perform usual activities.
Pain and discomfort
- No pain or discomfort.
- Moderate pain or discomfort.
- Extreme pain or discomfort.
Anxiety and depression
- Not anxious or depressed.
- Moderately anxious or depressed.
- Extremely anxious or depressed.
The attributes, which in this case are levels within each dimension and interactions between the dimensions, are combined using a mathematical function. In the case of the EQ-5D, there are a number of value sets that have been calculated and published (Szende, Oppe and Devlin, 2007), of which the most widely-known and used is taken from the UK Measuring and Valuing Health project undertaken at the University of York, based on the time trade-off method (Dolan, 1997). The mathematical form used by this is additive, which means that the attributes are weighted and added together. A newer version, the EQ-5D-5L (Herdman et al, 2011), has been published with the same dimensions, each of which has five levels.
QALYs involve the summing over time of quality of life at different points in time. In principle, if QALYs are to be used in an economic evaluation, QALYs that are generated at different times should be discounted if they are to be added together, in exactly the same way as costs are. There are arguments in favour of discounting both costs and QALYs at the same rate, discounting costs but not QALYs, and discounting them both, but at different rates. Current guidelines in the UK, for example from NICE, are to discount both at the same rate, the rate that is set by the UK Finance Ministry, HM Treasury, for measuring costs and monetary benefits in appraising public sector projects.
5.5.2 Monetary measures of benefit
For most goods and services, it is assumed that the prices that people are willing to pay reflect the value of the benefits that they obtain from them. So, a monetary value of a good or service can be estimated from information about whether people purchase it at particular prices and how much of it. For goods and services that are not marketed, this is not possible, so estimates of monetary measures of benefit are based on two main techniques: revealed preference and stated preference. For revealed preference, observations from people’s behaviour on other markets are used to infer monetary values. For example, researchers have estimated the value that people place on the avoidance of death or injury using job market data. They have compared the wages paid to people in jobs that differ in the risk of death and injury occurring but are otherwise identical. By contrast, stated preference techniques use surveys and experiments in which people are asked what monetary value they place on health benefits. Researchers usually do not ask that question directly, but give choices between different alternatives, whose descriptions include money values. Money values are inferred from the choices that they make.
Such stated preference studies are sometimes called willingness-to-pay studies, although that description is not always accurate. The economic theory underlying these kinds of studies is the measurement of what are called compensating variation and equivalent variation. In this context, they mean respectively monetary compensation made to a person for a change in health and monetary compensation to a person for keeping their existing state of health. Willingness to pay refers to compensation paid by the respondent, either for obtaining an improvement in their health or not having their health deteriorate. Willingness to accept refers to compensation paid to the respondent, either for having their health deteriorate or not obtaining an improvement in their health.
There are several different ways to carry out such studies, but best practice in economics more generally is to use the contingent valuation method. Contingent valuation requires the survey or experiment to include a description of a plausible market in which the choices made by respondents about goods reveal the values that are required. The values are then said to be contingent on that description.
5.6 Economic appraisal models and uncertainty
A possible approach to economic appraisal would be to use one source of data on resource use, costs and quality of life, for example a clinical trial in which these are all measured for individual patients. This would have the advantages that a clinical trial provides in terms of replicability of results. However, economic appraisals are far more usually based on different data sources that are linked together using an economic evaluation model, and in practice all health care appraisals involve at least some modelling. Economic modelling is regarded by many as superior to a trial-based economic appraisal, as it may overcome the problems that trials have such as the lack of generalisability and the long times that must elapse before they can produce usable results (Buxton et al, 1997; Halpern et al, 1998).
Economic evaluation models are usually much more complex than simply simply balance sheets that add up cost and benefit data to produce totals. Many economic appraisals cannot use such simple models, which are not acceptable to bodies such as NICE in the context of technology appraisals. Treatment options are not always straightforward and clinical decision making may involve strategies for management, rather than a simple choice between using and not using a single therapy. Moreover, there is usually considerable uncertainty about both the form that the model should take and the data that it uses.
Modelling usually uses decision analysis, described in section 7, which deals with both the complexity issue, by imposing a structure on the implied clinical decision making, and some aspects of uncertainty. However, one aspect of uncertainty, about the values that data take, is not dealt with directly by decision analysis. The issue is best explained by the observation that summaries of effectiveness data, such as changes in blood pressure resulting from some intervention, are usually presented as both a point estimate and an interval estimate, or confidence interval, reflecting variability in the data. Since there is variability in cost and effectiveness data, we should similarly summarise their distribution. When this is achieved as part of a trial-based appraisal it is called stochastic cost-effectiveness analysis.
Unfortunately, this has two problems. First, many of the data used in an appraisal model are in practice not properly based on statistically-based sampling, and do not have a variance that can be used to create an interval estimate. Secondly, the key summary index of cost-effectiveness, the ICER, is a ratio. In general, it is not possible to estimate a confidence interval for this even if all of the data that are used to calculate it have variances that can be calculated. This second problem applies equally to trial-based and model based analyses.
Uncertainty in models is usually dealt by sensitivity analysis, which is a set of techniques that analyse how sensitive results are to different specifications of the model, for example different values for the data that are contained within it or alternative assumptions about how the data should be combined. In the sensitivity analysis techniques that are described below, the model that has the best assumed structure and data is called the base case, and the assumptions and data that we wish to test are called the parameters of the model.
One-way sensitivity analysis looks at how sensitive results are to changes in one parameter. For example, if a new drug therapy is appraised using a model, one of the parameters of the model will be the unit cost of the drug. The base case will calculate an ICER using the best estimate that the analyst has of the unit cost. One-way sensitivity analysis calculates the ICER for different estimates of the unit costs, showing whether the cost makes a lot or a little difference to the result.
However, this is only helpful if we can give a meaning to ‘a lot’ or ‘a little’ that will enable us to judge whether the difference matters in the context of decision making. One way to do this is to use the ceiling ratio described in section 5.3.4. If the ICER is above or alternatively below the ceiling ratio at every possible value of the parameter, then the decision is not sensitive to the parameter’s value. In other cases, the ICER will be below the ceiling ratio for some levels of the parameter - in our drug example, perhaps when the unit cost is low - but at others above, - perhaps when the unit cost is high. Where the ICER is equal to the ceiling ratio, a change in the preferred option occurs. That point is called a threshold, and this process is known as threshold analysis. If the base case and the threshold are very different, then it can be concluded the results are not sensitive to the values of the parameter.
This is again only helpful if we can give a meaning to ‘very different’. One way is to define upper and lower plausible values for the parameter. For example, with a base case cost of £100 per unit, it may be thought unlikely that the cost could be as high as £200 or as low as £10, which defines a plausible range for the calculated ICER. If the threshold is within that range, then the results are sensitive to the assumption made.
Two-way analysis extends this to varying two parameters at the same time and observing their joint effect on the ICER. The ceiling ratio can again be used to define a threshold, and plausible ranges for the ICER can be calculated from the plausible values of the variables, taken in combination. This can be extended in theory to any number of parameters, but the analysis becomes difficult to conduct and interpret when there are more than three at the same time, though of course many different two-way and three-way analyses could be undertaken. Nevertheless, such multi-way analysis is essential, because it is possible, for example, that separate one way analyses of two parameters might lead an analyst to conclude that the results are not sensitive to their values, but some combinations of their plausible values might cause the ICER to take values outside the threshold.
5.6.2 Statistical sensitivity analysis
Unfortunately, plausible range methods are often unsatisfactory because their basis may be unclear and not testable. It is better to use statistically-based methods because, as suggested, the base case cost-effectiveness results can be treated as a point estimate and the results of sensitivity analysis form an interval estimate. This is called probabilistic sensitivity analysis.
This requires a distribution to be generated for the ICER using Monte Carlo simulations. A distribution for each of the model’s parameters is defined; if it not from an actual empirical estimate, its form may be assumed. Samples for each parameter are taken from their distribution, and the evaluation model uses those simulated data to calculate an ICER. This is repeated many times to generate an ICER distribution. In principle, it is then possible to calculate a variance and therefore an interval estimate.
Unfortunately, there is another problem with ICERs. Their distribution might spread over more than one quadrant of the CE plane, and include both positive and negative values. Positive and negative values mean such very different things (see section 5.3.4) that an interval estimate calculated from them is meaningless.
One solution to this problem is to use the net benefit approach described earlier. Net benefit is a single number, not a ratio, so there is no problem with using simulation to generate a distribution for it and calculate a variance and interval estimate. Another solution is to generate a cost-effectiveness acceptability curve (CEAC), which retains the ICER, but offers a different way of describing uncertainty (van Hout et al, 1994). Each simulated ICER value is compared with a ceiling ratio, and the proportion of simulated values that are acceptable at that ratio is calculated. This is repeated for each possible value of the ceiling ratio; the proportion that is acceptable will be different for each of those values. A CEAC plots these together, as in this diagram:
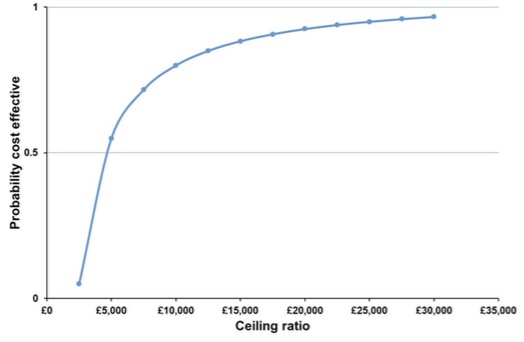
In this diagram, the proportion that is cost-effective is labelled the probability that the intervention is cost-effective. However, the interpretation of a proportion as a probability is only true under certain circumstances that are beyond the scope of this basic guide.
© David Parkin 2017
