Introduction
Learning objectives:
You will learn how to control for confounding in the design and analysis of a trial, and effect modification. This section assumes prior knowledge of the basic concept of confounding factors and measuring risk. Here confounding is briefly described, followed by methods for controlling for confounding at the design and analysis stage. Finally, effect modification is explained. Read the resource text below.
Resource text
Confounding: a recap Potential confounding variables always have to be considered in the design and analysis of epidemiological studies. Confounding occurs when a confounding variable, C, is associated with the exposure, E, and also influences the disease outcome, D.
Figure 1: Situation in which C may confound the affect of the E to D association [1].
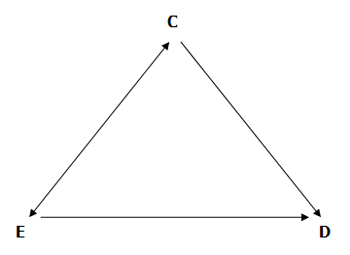
(Taken from Kirkwood and Sterne 2003). An epidemiological study wishes to investigate the E to D relationship, but the E to C and C to D associations may bias the estimate of the E to D association unless they are considered in the design or analysis. An example of confounding: When examining the relationship between alcohol consumption (E) and heart disease (D), smoking (C) would be an important confounding factor, since smoking is correlated with alcohol consumption and smoking is associated with heart disease [2].
Issues when controlling for confounders Referring back to Figure 1: a variable that is part of the causal chain leading from E to D is not a confounding factor. If E effects C which in turn effects D then we should not adjust for C since it is on the casual pathway to D. An example would be smoking in pregnancy (C) when examining socio-economic differences (E) in risk of low birth weight (D). This is because smoking is on the causal pathway to low birth weight. If we were to control for this there could be an underestimation of socio-economic factors.
Controlling for confounding A number of methods can be applied to control for potential confounding factors, both at the design stage and in the analysis of epidemiological studies. The aim is to make the groups as similar as possible with respect to the confounder. At the design stage, potential confounding factors may be identified based on previous studies or because the factor may be considered as biologically plausible.
Methods used for controlling for confounding at the design stage Restriction Restriction is a method that limits participation in the study to individuals who are similar in relation to the confounder. For example, a study restricted to non-smokers only will eliminate any confounding effect of smoking. However, a disadvantage of restriction is that it may be difficult to generalize to the rest of the population based on a homogeneous study group [3].
Matching in case control studies Matching involves selecting controls so that the distribution of potential confounders among them will be similar to those of the cases.
Randomization (random allocation) Involves the random allocation (e.g. using a table of random numbers) of individuals to exposure categories. Therefore, the distribution of known and unknown confounding variables will be similar for each of the groups being compared. This method may only be used in clinical trials.
Methods used for controlling for confounding during analysis
Methods to detect the presence of confounding The presence or magnitude of confounding in epidemiological studies is evaluated by observing the degree of discrepancy between the crude and adjusted estimates. One method to assess for the presence of confounding is to calculate the crude relative risk (without controlling for confounding) and compare this measure with the relative risk adjusted for the potential confounder. If the relative risk has changed and there is little variation between the stratum specific rate ratios, then there is evidence of confounding Note that it is inappropriate to use statistical methods to test for the presence of confounding.
Stratification Stratification allows the association between exposure and outcome to be examined within different strata of the confounding variable. For example by age, sex or alcohol consumption.
If we were conducting a study to examine the association between lung cancer and urban atmospheric pollution, controlling for smoking, the population could be stratified according to smoking status. The association between air pollution and cancer can then be assessed separately within each stratum [4].
Stratification allows for the assessment of modifying effects as well as controlling for confounding factors; e.g. stratification makes it possible to examine the effect of smoking on the association between atmospheric pollution and lung cancer.
The problem with simply creating strata is that in general, strata with more individuals will tend to have a more precise estimate of the association (with a smaller standard error) than strata with fewer individuals. Therefore we calculate a weighted average where greater weight is given to the strata with more data. The most common weighting scheme used is the Mantel-Haenszel method [1].
When using the Mantel-Haenszel method, an overall estimate of the relative risk adjusted for the potential confounder can be calculated by pooling the stratum specific rates. This gives us an overall summary measure of effect [1].
Mantel-Haenszel estimates can be calculated using all of the usual statistical packages. See related links for a relevant chapter on stratifying results using the Mantel-Haenszel method in a user friendly statistics textbook, and a link to a textbook that can help you to use these methods in a popular statistics package.
Standardisation The methods of direct and indirect standardisation are commonly used to control for the confounding affects of age and sex. (See section 3 on Standardisation).
Multivariate analysis As the number of confounders that can be controlled for simultaneously is limited, and particularly since this may lead to small numbers in some strata, statistical modelling (e.g. logistic regression) is commonly used to control for more than one confounder at the same time.
Beyond confounding
Effect modification (Interaction) Effect modification occurs when the effect of an exposure is different among different subgroups. For instance, if we were examining the relationship between obesity and mortality then we could say that gender or ethnicity are effect modifiers, since the effect of obesity on mortality varies according to gender and ethnicity. Another example could be immunisation status as an effect modifier on the relationship between exposure to a pathogen and outcome [1].
Another term for effect modification is interaction. Interaction occurs when the direction or magnitude of an association between two variables differs due to the effect of a third variable. It can reflect a cumulative effect of multiple risk factors that are not acting independently, and can produce a greater or lesser effect than the sum of the effects of each factor acting on its own.
When using Mantel-Haenszel methods for stratification, an important assumption is made, namely that there is no effect modification occurring. If effect modification is occurring then there is little point in combining the weighted strata to achieve an overall measure, and a more sophisticated method of stratification should be used.
References 1. Kirkwood, B.R. Sterne, J.C. 2003. Essential Medical Statistics. Blackwell Science. 2. Farmer, R. Lawrenson, R. 2004. Lecture notes in Epidemiology and Public Health Medicine pp 67-68. Blackwell Publishing. 3. Hennekens CH, Buring JE. 1987. Epidemiology in Medicine, Lippincott Williams & Wilkins. 4. Last, J.M. A dictionary of epidemiology. p78. 4th Edition. Oxford University Press 2001. 5. Baron, J. A., Gerhardsson de Verdier, M., Ekbom, A. Coffee, tea, tobacco, and cancer of the large bowel. Cancer Epidemiol Biomarkers Prev. 1994, 3: 565-70. 6. Tavani, A., Pregnolato, A., La Vecchia, C., Negri, E., Talamini, R., Franceschi, S. Coffee and tea intake and risk of cancers of the colon and rectum: a study of 3,530 cases and 7,057 controls. Int J Cancer. 1997, 73: 193-7.
Related links Mantel-Haenszal estimates:additional reading on this topic Kirkwood, B.R. Sterne, J.C. 2003. Essential Medical Statistics. pp170-188 Blackwell Science. Dupont, W.D. Statistical Modeling for Biomedical Researchers. pp145-150.Cambridge University Press 2002.
