Measures of Location and Dispersion and their appropriate uses

Statistics: Measures of location and dispersion

This section covers

Mean
Median
Mode
Range
Interquartile Range
Standard deviation

Measures of Location

Measures of location describe the central tendency of the data. They include the mean, median and mode.

Mean or Average

The (arithmetic) mean, or average, of n observations 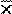(pronounced “x bar”) is simply the sum of the observations divided by the number of observations; thus:

\(\bar x = \frac{{{\rm{Sum\;of\;all\;sample\;values}}}}{{{\rm{Sample\;size}}}} = \;\frac{{\sum {x_i}}}{n}\)

In this equation, xi represents the individual sample values and Σxi their sum. The Greek letter 'Σ' (sigma) is the Greek capital 'S' and stands for 'sum'. Their calculation is described in example 1, below.

Median

The median is defined as the middle point of the ordered data. It is estimated by first ordering the data from smallest to largest, and then counting upwards for half the observations. The estimate of the median is either the observation at the centre of the ordering in the case of an odd number of observations, or the simple average of the middle two observations if the total number of observations is even. More specifically, if there are an odd number of observations, it is the [(n+1)/2]th observation, and if there are an even number of observations, it is the average of the [n/2]th and the [(n/2)+1]th observations.

Example 1 Calculation of mean and median

Consider the following 5 birth weights, in kilograms, recorded to 1 decimal place:

1.2, 1.3, 1.4, 1.5, 2.1

The mean is defined as the sum of the observations divided by the number of observations. Thus mean = (1.2+1.3+…+2.1)/5 = 1.50kg. It is usual to quote 1 more decimal place for the mean than the data recorded.

There are 5 observations, which is an odd number, so the median value is the (5+1)/2 = 3rd observation, which is 1.4kg. Remember that if the number of observations was even, then the median is defined as the average of the [n/2]th and the [(n/2)+1]th. Thus, if we had observed an additional value of 3.5kg in the birth weights sample, the median would be the average of the 3rd and the 4th observation in the ranking, namely the average of 1.4 and 1.5, which is 1.45kg.

Advantages and disadvantages of the mean and median

The major advantage of the mean is that it uses all the data values, and is, in a statistical sense, efficient.

The main disadvantage of the mean is that it is vulnerable to outliers. Outliers are single observations which, if excluded from the calculations, have noticeable influence on the results. For example, if we had entered '21' instead of '2.1' in the calculation of the mean in Example 1, we would find the mean changed from 1.50kg to 7.98kg. It does not necessarily follow, however, that outliers should be excluded from the final data summary, or that they always result from an erroneous measurement.

The median has the advantage that it is not affected by outliers, so for example the median in the example would be unaffected by replacing '2.1' with '21'. However, it is not statistically efficient, as it does not make use of all the individual data values.

Mode

A third measure of location is the mode. This is the value that occurs most frequently, or, if the data are grouped, the grouping with the highest frequency. It is not used much in statistical analysis, since its value depends on the accuracy with which the data are measured; although it may be useful for categorical data to describe the most frequent category. The expression 'bimodal' distribution is used to describe a distribution with two peaks in it. This can be caused by mixing populations. For example, height might appear bimodal if one had men and women on the population. Some illnesses may raise a biochemical measure, so in a population containing healthy and ill people one might expect a bimodal distribution. However, some illnesses are defined by the measure (e.g. obesity or high blood pressure) and in this case the distributions are usually unimodal.

Measures of Dispersion or Variability

Measures of dispersion describe the spread of the data. They include the range, interquartile range, standard deviation and variance.

Range and Interquartile Range

The range is given as the smallest and largest observations. This is the simplest measure of variability. Note in statistics (unlike physics) a range is given by two numbers, not the difference between the smallest and largest. For some data it is very useful, because one would want to know these numbers, for example knowing in a sample the ages of youngest and oldest participant. If outliers are present it may give a distorted impression of the variability of the data, since only two observations are included in the estimate.

Quartiles and Interquartile Range

The quartiles, namely the lower quartile, the median and the upper quartile, divide the data into four equal parts; that is there will be approximately equal numbers of observations in the four sections (and exactly equal if the sample size is divisible by four and the measures are all distinct). Note that there are in fact only three quartiles and these are points not proportions. It is a common misuse of language to refer to being ‘in the top quartile’. Instead one should refer to being ‘in the top quarter or ‘above the top quartile’. However, the meaning of the first statement is clear and so the distinction is really only useful to display a superior knowledge of statistics! The quartiles are calculated in a similar way to the median; first arrange the data in size order and determine the median, using the method described above. Now split the data in two (the lower half and upper half, based on the median). The first quartile is the middle observation of the lower half, and the third quartile is the middle observation of the upper half. This process is demonstrated in Example 2, below.

The interquartile range is a useful measure of variability and is given by the lower and upper quartiles. The interquartile range is not vulnerable to outliers and, whatever the distribution of the data, we know that 50% of observations lie within the interquartile range.

Example 2 Calculation of the quartiles

Suppose we had 18 birth weights arranged in increasing order.

1.51, 1.53. 1.55, 1.55, 1.79. 1.81, 2.10, 2.15, 2.18,

2.22, 2.35, 2.37, 2.40, 2.40, 2.45, 2.78. 2.81, 2.85.

The median is the average of the 9th and 10th observations (2.18+2.22)/2 = 2.20 kg. The first half of the data has 9 observations so the first quartile is the 5th observation, namely 1.79kg. Similarly the 3rd quartile would be the 5th observation in the upper half of the data, or the 14th observation, namely 2.40 kg. Hence the interquartile range is 1.79 to 2.40 kg.

Standard Deviation and Variance

The standard deviation of a sample (s) is calculated as follows:

\(s = \;\sqrt {\frac{{\sum {{\left( {{x_i} - \bar x} \right)}^2}}}{{n - 1}}}\)

The expression ∑(x_i- 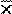)² is interpreted as: from each individual observation (x_i) subtract the mean (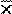), then square this difference. Next add each of the n squared differences. This sum is then divided by (n-1). This expression is known as the sample variance (s²). The variance is expressed in square units, so we take the square root to return to the original units, which gives the standard deviation, s. Examining this expression it can be seen that if all the observations were the same (i.e. x_{1 =}x_{2 =}x_{3 ... =}x_n), then they would equal the mean, and so s would be zero. If the x's were widely scattered about, then s would be large. In this way, s reflects the variability in the data. The calculation of the standard deviation is described in Example 3. The standard deviation is vulnerable to outliers, so if the 2.1 was replace by 21 in Example 3 we would get a very different result.

Example 3 Calculation of the standard deviation

Consider the data from example 1. The calculations required to determine the sum of the squared differences from the mean are given in Table 1, below. We found the mean to be 1.5kg. We subtract this from each of the observations. Note the mean of this column is zero. This will always be the case: the positive deviations from the mean cancel the negative ones. A convenient method for removing the negative signs is squaring the deviations, which is given in the next column. These values are then summed to get a value of 0.50 kg². We need to find the average squared deviation. Common-sense would suggest dividing by n, but it turns out that this actually gives an estimate of the population variance, which is too small. This is because we are using the estimated mean 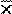in the calculation and we should really be using the true population mean. It can be shown that it is better to divide by the degrees of freedom, which is n minus the number of estimated parameters, in this case n-1. An intuitive way of looking at this is to suppose one had n telephone poles each 100 meters apart. How much wire would one need to link them? As with variation, here we are not interested in where the telegraph poles are, but simply how far apart they are. A moment's thought should convince one that n-1 lengths of wire are required to link n telegraph poles.

Table 1 Calculation of the mean squared deviation

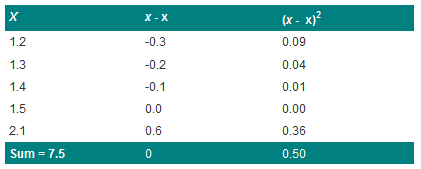
From the results calculated thus far, we can determine the variance and standard deviation, as follows:

n = 5

Variance = 0.50/(5-1) = 0.125 kg²

Standard deviation = √(0.125) = 0.35 kg

Why is the standard deviation useful?

It turns out in many situations that about 95% of observations will be within two standard deviations of the mean, known as a reference interval. It is this characteristic of the standard deviation which makes it so useful. It holds for a large number of measurements commonly made in medicine. In particular, it holds for data that follow a Normal distribution. Standard deviations should not be used for highly skewed data, such as counts or bounded data, since they do not illustrate a meaningful measure of variation, and instead an IQR or range should be used. In particular, if the standard deviation is of a similar size to the mean, then the SD is not an informative summary measure, save to indicate that the data are skewed.

Standard deviation is often abbreviated to SD in the medical literature.

Reference

Campbell MJ, Machin D and Walters SJ. Medical Statistics: a Commonsense Approach 4th ed. Chichester: Wiley-Blackwell 2007